Tutorial: Steps In The Design Of A 2-Way Spanning Slab With BS8110
Let’s talk about Slab Design…
How can you design a 2 way spanning slab and be able to know the reinforcement size to be used in your slab as well as the spacing needed when tieing your reinforcements.
So on this post, you’ll be able to have a clue on how to design a 2 way spanning slab. You’ll know the following:
How to determine the Ultimate Load, F
How to calculate the dead load
How to determine the ratio ly/lx
How to check for deflection.
Now let’s begin…..!
Let’s assume you’re given a part floor plan for a residential building just as I’m going to draw below. Let’s also assume the floor consist of a 150mm thick slab cast insitu with edge beams. Also assume the design data which I’m going to list below have been provided for you as a young practicing engineer.
Now how do you design a 2 way spanning slab?
Check out the design data given below:
Design Data
Characteristic live load, Qk = 1.5KN/m²
Partitioning, Let’s Assume. = 1.1KN/m²
Finishing, Say. = 1.2KN/m²
Concrete Grade (fcu). = 20KN/m²
Characteristic strength of steel (mild), fy. = 250KN/m²
Concrete Cover, c = 20mm
Solution
Let’s determine the loading
Concrete own weight (0.15 x 24) = 3.6KN/m²
Partitioning = 1.1KN/m²
Finishing. = 1.2KN/m²
______________________________________________________
Total Dead Load, Gk. = 5.9KN/m²
______________________________________________________
Ultimate Load, F:
F = 1.4Gk + 1.6Qk
But Gk = 5.9KN/m², Qk = 1.5KN/m²
Therefore: F = (1.4 x 5.9) + (1.6 x 1.5)
Ultimate load, F = 10.66KN/m²
Determine the Ratio ly/lx
Ratio ly/lx is determine by dividing the longest span of the slab by the shorter span.
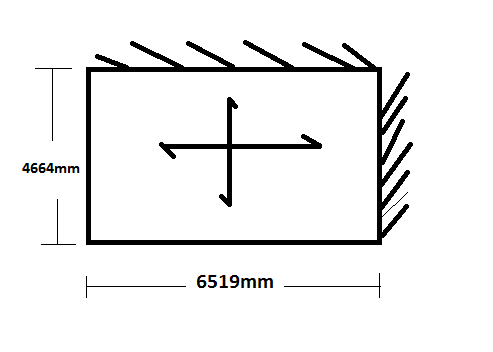
The shortest as well as longest span can be known by looking at the dimensions of the slab as shown below.
For the slab in question, ly = 6519: lx = 4664
Therefore 6519/4664 = 1.4
>>Effective Depth = thickness – concrete cover – 1/2 bar size
d = 150-20-10/2 = 125mm
>>Determine the Moment
Short Span: (Edge (B) = 0.074, Span = 0.055 ( Obtained from the BS Code)
M = Bwlx² = Bflx²
Mid span: m = 0.055 x 10.66 x 4.664²
M = 12.75KNm
Continuous Edge: M = 0.074 x 10.66 x 4.664²
M = 17.16 KNm
Long Span: (edge (B) = 0.045, span (B) = 0.034)
M = Bflx²
Mid Span: m = 0.034 x 10.66 x 4.664²
= 7.9KNm
Continuous Edge: m = 0.045 x 10.66 x 4.664²
= 10.44KNm
Design Proper….!
Short Span
Mid-Span: K = (m/fcubd²) = (12.75 x 106)/20 x 1000 x 125²
K = 0.041
Lever Arm, la = 0.5 + √0.25 – (k/0.9) = 0.5 + √0.25 -(0.041/0.9)
La = 0.95
As = M/0.95fylad = 12.75 x 10^6/0.95 x 250 x 0.95 x 125
As = 452mm²
Provide Y12 @200mm c/c Btm (566mm²)
Continuous Edge:
K = (M x 16 x 106)/20 x 1000 x 125²
K = 0.055
Lever Arm, la = 0.5 + √0.25 – (k/0.9) = 0.5 + √0.25 -(0.055/0.9).
La = 0.94
As = (17.16 x 10 ^6)/(0.95 x 250 x 0.94 x 125)
As = 614.9 or 615mm²
Provide Y12 @ 150mm c/c btm (754mm²)
Long Span
Mid-span: K = (7.9 x 106)/(20 x 1000 x 125²)
K = 0.024
Lever Arm, la = 0.5 + √0.25 – (k/0.9) = 0.5 + √0.25 -(0.024/0.9)
= 0.97
Since LA value is greater than 0.95, we use 0.95
As = (7.9 x 106)/(0.95 x 250 x 0.95 x 125)
As = 280mm²
Provide Y10 @ 200mm c/c top (393mm²)
Continuous Edge
K = 10.44 x 106/20 x 1000 x 125²
K = 0.033
Lever Arm, la = 0.5 + √0.25 – (k/0.9) = 0.5 + √0.25 -(0.033/0.9)
La = 0.96
But we use, la = 0.95
As = 10.44 x 106/(0.95 x 250 x 0.95 x125)
As = 370mm²
Provide Y12 @225mm c/c top (502mm²)
Check For Deflection
Fs = 2AsReq/3As Provided
Fs = (2 x 250 x 452)/(3 x 566) = 133.1 deflection is OK
So this is how to design a 2 way spanning slab using BS8110
As you can see all the parameters has been carefully analysed and solved for so you can follow this step if you ever encounter a 2 way spanning slab in your design process.
Please Note:
1. This will only be familiar to those that are used to the basics of structural design.
2. The design Data are values selected before you begin to design
3. Parameters will be explained in other articles on this blog so keep a date with us.




where do you get the table for area of steel so as to find the reinforcement required?
BS Code…
If you're a Nigerian, you can find it on Victor Oyenuga's Textbook